(자바스크립트 알고리즘) 최대공약수와 최소공배수 - kimyang-sun

자바스크립트 알고리즘 (Programmers)

최대공약수와 최소공배수!

---

문제 설명

두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.

 

제한 조건

• 두 수는 1이상 1000000이하의 자연수입니다.

입출력 예

---

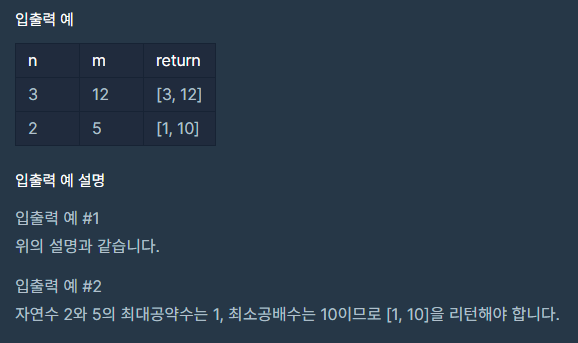
문제 풀이

function solution(n, m) {
    const gcd = (a, b) => a % b === 0 ? b : gcd(b, a % b);
    const lcm = (a, b) => a * b / gcd(a, b);
    return [gcd(n, m), lcm(n, m)];
}

풀이입니다.

 

최대공약수인 gcd 와 최소공배수인 lcm 을 함수로 미리 만들어두고

 

배열로 리턴하였습니다.

 

우선 최대공약수는 유클리드 호제법을 이용하였습니다.

 

유클리드 호제법의 원리입니다.

 

2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b)

a와 b의 최대공약수는 b와 r의 최대공약수와 같습니다.

이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고,

다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수입니다.

 

최소공배수는 두 수를 곱한 후에 최대공약수로 나누면 나옵니다.

 

다른 사람들의 풀이

function gcdlcm(a, b) {
  var gcd = calc_gcd(a, b);
  var lcm = (a * b) / gcd;

    return [gcd, lcm];
}

function calc_gcd(a, b) {
  if (b == 0) return a;
    return a > b ? calc_gcd(b, a % b) : calc_gcd(a, b % a);
}